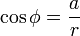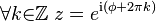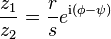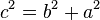Media aritmética
Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación.
En matemáticas y estadística, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoriarecibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.
Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.
También la media aritmética puede ser denominada como centro de gravedad de una distribución, el cual no esta necesariamente en la mitad.
Una de las limitaciones de la media aritmética es que se trata de una medida muy sensible a los valores extremos; valores muy altos tienden a aumentarla mientras que valores muy bajos tienden a reducirla, lo que implica que puede dejar de ser representativa de la población.
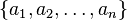 , la media aritmética se define simplemente como:
, la media aritmética se define simplemente como:
Definición
Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra (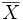 ), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
Propiedades
- La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica:
- La media aritmética está comprendida entre el valor máximo y el valor mínimo del conjunto de datos:
Sucesiones y Progresiones
Una sucesión es un conjunto de números dispuestos uno a continuación de otro.
a1, a2, a3 ,..., an
Los números a1, a2 , a3 , ...; se llaman términos de la sucesión.
El subíndice indica el lugar que el término ocupa en la sucesión.
El término general es an es un criterio que nos permite determinar cualquier término de la sucesión.
Determinación de una sucesión:
Por el término general
an= 2n-1
Por una ley de recurrencia
Los términos se obtienen operando con los anteriores.
Operaciones con sucesiones
Dadas las sucesiones an y bn:
an= a1, a2, a3, ..., an
bn= b1, b2, b3, ..., bn
Suma con sucesiones:
(an) + (bn) = (an + bn)
(an) + (bn) = (a1 + b1, a2 + b2, a3 + b3, ..., an + bn)
Propiedades
1 Asociativa:
(an + bn) + cn = an + (bn + c n)
2 Conmutativa:
an + bn = bn + a n
3 Elemento neutro
(0) = (0, 0, 0, ..)
an + 0 = an
4 Sucesión opuesta
(-an) = (-a1, -a2, -a3, ..., -an)
an + (-an) = 0
Diferencia con sucesiones:
(an) - (bn) = (an - bn)
(an) - (bn) = (a1 - b1, a2 - b2, a3 - b3, ..., an - bn)
Producto con sucesiones:
(an) · (bn) = (an · bn)
(an) · (bn) = (a1 · b1, a2 · b2, a3 · b3, ..., an · bn)
Propiedades
1 Asociativa:
(an · bn) · c n = an · (bn · c n)
2 Conmutativa:
an · bn = bn · a n
3 Elemento neutro
(1) = (1, 1, 1, ..)
an · 1 = an
4 Distributiva respecto a la suma
an · (bn + c n) = an · bn + an · c n
Sucesión inversible
Una sucesión es inversible o invertible si todos sus términos son distintos de cero. Si la sucesión bn es inversible, su inversa es:

Cociente
Sólo es posible el cociente entre dos sucesiones si el denominador es inversible.

Límite de una sucesión
Es el número al cual se van aproximando los términos de una sucesión
Sucesiones convergentes
Son las que tienen límite.
Sucesiones divergentes
Son las sucesiones que no tienen límite finito.
Tipos de sucesiones
Sucesiones monótonas

Sucesiones estrictamente crecientes
Se dice que una sucesión es estrictamente creciente si cada término es mayor o igual que el anterior.
an+1 > an
Sucesiones crecientes
Se dice que una sucesión es creciente si cada término es mayor o igual que el anterior.
an+1 ≥ an
Sucesiones estrictamente decrecientes
Se dice que una sucesión es estrictamente decreciente si cada término de la sucesión es menor que el anterior.
an+1 < an
Sucesiones decrecientes
Se dice que una sucesión es decreciente si cada término de la sucesión es menor o igual que el anterior.
an+1 ≤ an
Sucesiones constantes
Se dice que una sucesión es constante si todos su términos son iguales, an= k.
an = an+1
Sucesiones acotadas inferiormente
Una sucesión está acotada inferiormente si todos sus términos son mayores o iguales que un cierto número K, que llamaremos cota inferior de la sucesión.
an ≥ k
A la mayor de las cotas inferiores se le llama extremo inferior o ínfimo .
Si el ínfimo de una sucesión es uno de sus términos se le llama mínimo.
Toda sucesión acotada inferiormente es creciente.
Sucesiones acotadas superiormente
Una sucesión está acotada superiormente si todos sus términos son menores o iguales que un cierto número K', que llamaremos cota superior de la sucesión.
an ≤ k'
A la menor de las cotas superiores se le llama extremo superior o supremo.
Si el supremo de una sucesión es uno de sus términos se llama máximo.
Toda sucesión acotada superiormente es monótona decreciente.
Sucesiones acotadas
Una sucesión se dice acotada si está acotada superior e inferiormente. Es decir si hay un número k menor o igual que todos los términos de la sucesión y otro K' mayor o igual que todos los términos de la sucesión. Por lo que todos los términos de la sucesión están comprendidos entre k y K'.
k ≤ an ≤ K'
Progresiones aritméticas
Una progresión aritmética es una sucesión de números tales que cada uno de ellos (salvo el primero) es igual al anterior más un número fijo llamado diferencia que se representa por d.
Término general de una progresión aritmética
1 Si conocemos el 1er término.
an = a1 + (n - 1) · d
2 Si conocemos el valor que ocupa cualquier otro término de la progresión.
an = ak + (n - k) · d
Interpolación de términos
Interpolar medios diferenciales o aritméticos entre dos números, es construir una progresión aritmética que tenga por extremos los números dados.
Sean los extremos a y b, y el número de medios a interpolar m.
![]()
Suma de términos equidistantes
Sean ai y aj dos términos equidistantes de los extremos, se cumple que la suma de términos equidistantes es igual a la suma de los extremos.
ai + aj = a1 + an
![]()
a3 + an-2 = a2 + an-1 = a1 + an
Suma de n términos consecutivos
![]()
Progresiones geométricas
Una progresión geométrica es una sucesión en la que cada término se obtiene multiplicando al anterior una cantidad fija r, llamada razón.
![]()
Término general de una progresión geométrica
1 Si conocemos el 1er término.
an = a1 · rn-1
2 Si conocemos el valor que ocupa cualquier otro término de la progresión.
an = ak · rn-k
Interpolación de términos
Interpolar medios geométricos o proporcionales entre dos números, es construir una progresión geométrica que tenga por extremos los números dados.
![]()
Suma de n términos consecutivos
![]()
Suma de los términos de una progresión geométrica decreciente
![]()
Producto de dos términos equidistantes
Sean ai y aj dos términos equidistantes de los extremos, se cumple que el producto de términos equidistantes es igual al producto de los extremos.
ai . aj = a1 . an
![]()
a3 · an-2 = a2 · an-1 = ... = a1 · an
Producto de n términos equidistantes
![]()
Término general de una sucesión
1 Comprobar si es una progresión aritmética.
2 Comprobar si es una progresión geométrica.
3 Comprobar si los términos son cuadrados perfectos.
También nos podemos encontrar con sucesiones cuyos términos son números próximos a cuadrados perfectos.
4 Si los términos de la sucesión cambian consecutivamente de signo.
Si los términos impares son negativos y los pares positivos: Multiplicamos an por (-1)n.
Si los términos impares son positivos y los pares negativos: Multiplicamos an por (-1)n-1.
5 Si los términos de la sucesión son fraccionarios (no siendo una progresión).
Se calcula el término general del numerador y denominador por separado.
Combinación lineal
Un vector  se dice que es combinación lineal de un conjunto de vectores
se dice que es combinación lineal de un conjunto de vectores  si existe una forma de expresarlo como suma de parte o todos los vectores de
si existe una forma de expresarlo como suma de parte o todos los vectores de  multiplicados cada uno de ellos por un coeficiente escalar
multiplicados cada uno de ellos por un coeficiente escalar  , de forma que:
, de forma que:
.
Así,  es combinación lineal de vectores de
es combinación lineal de vectores de  si podemos expresar
si podemos expresar  como una suma de múltiplos de una cantidad finita de elementos de
como una suma de múltiplos de una cantidad finita de elementos de  .
.
Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir  sin más que despejar laz. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
sin más que despejar laz. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
En otras palabras, cuánto de cada vector del conjunto  necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector
necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector  en cuestión.
en cuestión.
[editar]Expansión lineal
Dado un conjunto de vectores  , finito o infinito, se llama expansión lineal, denotada como span(A) al conjunto:
, finito o infinito, se llama expansión lineal, denotada como span(A) al conjunto:
Dicho conjunto es el mínimo subespacio vectorial de  que contiene al conjunto
que contiene al conjunto  .
.
Módulo y Argumento
En esta representación,  es el módulo del número complejo y el ángulo
es el módulo del número complejo y el ángulo 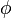 es el argumento del número complejo.
es el argumento del número complejo.
Formamos un triángulo rectángulo, con r como hipotenusa, y con catetos a y b. Vemos que:
Despejamos a y b en las expresiones anteriores y, utilizando la representación binomial:
Sacamos factor común r:
Frecuentemente, esta expresión se abrevia convenientemente de la siguiente manera:
la cual solo contiene las abreviaturas de las razones trigonométricas coseno, la unidad imaginaria y la razón seno del argumento respectivamente.
Según esta expresión, puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.
Según la Fórmula de Euler, vemos que:
No obstante, el ángulo φ no está unívocamente determinado por z, como implica la fórmula de Euler:
Por esto, generalmente restringimos φ al intervalo [-π, π) y a éste φ restringido lo llamamos argumento principal de z y escribimos φ = Arg(z). Con este convenio, las coordenadas estarían unívocamente determinadas por z.
La multiplicación de números complejos es especialmente sencilla con la notación polar:
División:
Potenciación:
Números Complejos
El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i). Los números complejos se utilizan en todos los campos de las matemáticas, en muchos de la física (y notoriamente en lamecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.
En matemáticas, los números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo. La propiedad más importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas.
Los números complejos son una extensión de los números reales, cumpliéndose que  . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
Los números complejos son la herramienta de trabajo del álgebra ordinaria, llamada álgebra de los números complejos, así como de ramas de las matemáticas puras y aplicadas como variable compleja, aerodinámica y electromagnetismo entre otras de gran importancia.
Contienen a los números reales y los imaginarios puros y constituyen una de las construcciones teóricas más importantes de la inteligencia humana. Los análogos del cálculo diferencial e integralcon números complejos reciben el nombre de variable compleja o análisis complejo.
Multiplicación de números complejos en forma binómica
El producto de los números complejos se realiza aplicando la propiedad distributiva del producto respecto de la suma y teniendo en cuenta que i2 = −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
( 5 + 2 i) · ( 2 − 3 i) =
=10 − 15i + 4i − 6 i2 = 10 − 11i + 6 = 16 − 11i
Multiplicación de números complejos en forma polar
La multiplicación de dos números complejos es otro número complejo tal que:
Su módulo es el producto de los módulos.
Su argumento es la suma de los argumentos.
645° · 315° = 1860°
Producto por un complejo de módulo 1
Al multiplicar un número complejo z = rα por 1β se gira z un ángulo β alrededor del origen.
rα · 1β = rα + β
TRIGONOMETRÏA
La trigonometría: es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Se deriva del vocablo griego τριγωνο <trigōno> "triángulo" + μετρον <metron> "medida".1
En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas enastronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Las funciones trigonométricas
La trigonometría como rama de las matemáticas realiza su estudio en la relación entre los lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones. Para el desarrollo de este fin se definieron una serie de funciones que han sobrepasado su fin original, convirtiéndose en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.
Teorema de Pitgoras
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
(1)
De la ecuación (1) se deducen fácilmente 3 fórmulas de aplicación práctica:
 |  |  |
Historia
El Teorema de Pitágoras lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros, pero no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.

Productos Notables-Binomios Conjugados
Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados y recíprocamente
El binomio conjugado de uno dado, es otro binomio que se diferencia únicamente por el signo de uno de los términos.
Por ejemplo: a – b es el binomio conjugado de a + b.
También se suele decir que a – b es el conjugado del binomio a + b.
Producto de dos binomios conjugados
El producto de dos binomios conjugados es un producto notable y su resultado es una diferencia de cuadrados perfectos:
Ejemplo:
(a+b) (a-b)=a2 - b2 (el numero 2 significa al cuadrado)
Ejemplo:
(-x+y) (x+y)= -x2 + y2 (el numero 2 significa al cuadrado)
Hallar el producto de los binomios conjugados:
(3x+4) (3x-4)
Solución: de acuerdo a la forma del producto de binomios conjugados:
(3x+4) (3x-4) = (3x)² - (4)² = 9x² - 16
Demostración de Identidades Trigonometricas
sen² x +cos² x =1 ..............(1)
Vamos a resolver las identidades
a) 1 + cos x / sen x = sen x / (1 - cos x)
Pasando cada denominador al otro miembro, tenemos
(1 + cos x) * (1-cos² x) = sen x * sen x
En el primer miembro tenemos una diferencia de cuadrados y en el segundo tenemos el seno elevado al cuadrado:
1 - cos² x = sen² x
Pasando cos² x al segundo miembro y transponiendo
sen² x + cos² x = 1
b) 1 - sen x = cos² x / (1 + sen x)
Pasando el denominador del segundo miembro al primero multiplicando:
(1 - sen x) * (1 + sen x) = cos² x
En el primer miembro también tenemos una diferencia de cuadrados:
1² - sen² x = cos² x
Pasando el segundo término del primer miembro al segundo miembro, cambiado de signo:
1 = sen² x + cos² x
que intercambiando nos queda igual a la fórmula (1)
sen² x + cos² x = 1
c) √(1 - cos² x) * √(1+ tan² x) * √(csc² x - 1) = 1
Elevando al cuadrado los dos miembros, nos queda
(1 - cos² x) * (1+ tan² x) * (csc² x - 1) = 1
Remplazando en el primer miembro por (1) y en el segundo y tercero por funciones equivalentes tan=sen/cos y csc=1/sen
sen² x * (1 + sen² x / cos² x) * [(1/sen² x ) - 1] = 1
sen² x * [(cos² x/cos² x) +(sen² x / cos² x)] * [(1 - sen² x)/sen² x)] = 1
Efectuando la suma en el segundo término y remplaando por (1) en el tercer término.
sen² x * [(cos² x + sen² x )/cos² x] * (cos² x)/sen² x = 1
sen² x * 1 / cos² x * cos²/sen² x = 1
(sen² x / cos²x) * (cos² x / sen² x) =1
Y simplificando
1 = 1
d) cos x + cos y = 2*cos (x+y/2) * cos (x-y/2)
Considerando las fórmulas de adción de ángulos
cos (α+ß) = cos α * cos ß - sen α * sen ß ..........(2)
cos (α-ß) = cos α * cos ß + sen α * sen ß...........(3)
Sumando y restando las fórmulas (2) y (3) se obtiene
sen α * cos ß = 1/2 * [(cos (α+ß) + cos (α-ß)]
Y poniendo α+ß=x ...y...α-ß=y ; es decir α=(x+y)/2.. y... ß=(x-y)/2, se obtienen las fórmulas de prostafóresis:
cs x + cos y = 2 * cos [(x+y)/2] * cos[(x-y)/2]
Espero que hayas comprendido el procedimiento
Simón Rodriguez
De la infancia de Rodríguez se conoce muy poco. El carácter nada común de este lo llevó a quitarse el apellido paterno y a quedarse sólo con el de su madre. En junio de 1814 se casó con María de los Santos Ronco, acto en el cual se declaró “expósito de esta feligresía”.
Desde muy joven, Simón Rodríguez se dedicó a la educación y gozó del honor de ser el maestro de Simón Bolívar, en quien influyó notablemente. Toda su vida estuvo acompañada de ideas revolucionarias. Simpatizó con el movimiento independentista de Gual y España, y ante su fracaso, también él debió emigrar. Entonces se dirigió a Jamaica, donde estudió la lengua inglesa. Partió luego a los Estados Unidos y, finalmente a Europa.
La estadía del maestro en el viejo continente le permitió dominar el francés, el italiano, el alemán y el portugués, profundizar sus estudios filosóficos y entrar en contacto con las teorías revolucionarias que pronto implantarían un nuevo orden político y social de alcance mundial. Todos estos conocimientos, más tarde los vertiría en su más destacado alumno: el Libertador Simón Bolívar.
En Francia se encontraron maestro y alumno y de allí partieron a un viaje que los llevó a Lyon y Chambery, para luego atravesar Los Alpes y entrar a Italia. En Milán, Rodríguez y Bolívar presenciarían la coronación de Napoléon Bonaparte como rey de Italia; y en Roma, el futuro Libertador de América se comprometería con el futuro de este continente, desencadenado del dominio español.
Rodríguez se separó de su alumno y a partir de 1806 inició una peregrinación por varios países de Europa.
De vuelta a América, Bogotá fue sede de la primera escuela-taller fundada por el maestro, en 1824. En 1825, Bolívar recibió a su mentor en Lima y lo incorporó a su grupo de colaboradores directos, nombrándolo “Director de Enseñanza Pública, Ciencias, Físicas, Matemáticas y de Artes y Director General de Minas, Agricultura y Caminos Públicos de la República Boliviana”.
El 7 de enero de 1826, Bolívar regresó a Lima y Rodríguez permaneció en Bolivia, de aquí no volverían a verse más. Aquel año fundó la segunda escuela-taller, con proyecciones para toda Bolivia. Su labor no pudo continuar debido a sus ásperas relaciones con el Presidente de Bolivia, Antonio José de Sucre. Rodríguez renunció a su cargo.
El maestro se marchó a Arequipa donde publicó el Pódromo de Sociedades americanas en 1828, obra en la que insistía en buscar soluciones propias para los problemas de Hispanoamérica.
Desde Lima, Rodríguez viajó en 1834 a Concepción (Chile) y allí se encuentra por segunda vez con Andrés Bello –ya se habían visto en Europa–. En Valparaiso escribió en el periódico El Mercurio. En 1842 viajó de Lima a Ecuador. De allí visitó varias localidades de suramérica dejando rastro de su talento y creación inagotable.
Simón Rodríguez murió en una aldea peruana en 1854, pobre y sin hogar. Sus restos fueron trasladados en 1954 al Panteón Nacional, en el centenario de su muerte.
Algunas de las obras de Simón Rodríguez son: Defensa de Bolívar; El Libertador del Mediodía de América y sus compañeros de armas,Defendidos por un amigo de la causa social; Observaciones sobre el terreno de Vincocaya; Luces y virtudes sociales.

Golf
Conocenos!

- Daviangela, Ginmar y Alexandra
- Guarenas, Menca, Venezuela
- Nosotras somos de 4to año, Seccion "A", Este es nuestro proyecto del RICON PATRIO en matematica.. Esta pagina la hicimos entre las 3 El diseño fue realizado por Ginmar luces unas de las titulares de nuestra paginas, cada semana nos ponemos de acuerdo para que cada una suban imformacion! Espero que le guste este blogeer y que lo disfruten! Gracias!




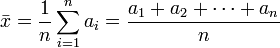
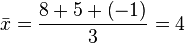
![\sqrt[n]{x_1 x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}](http://upload.wikimedia.org/math/8/e/6/8e601c29ce3964e378346560bff6a281.png)